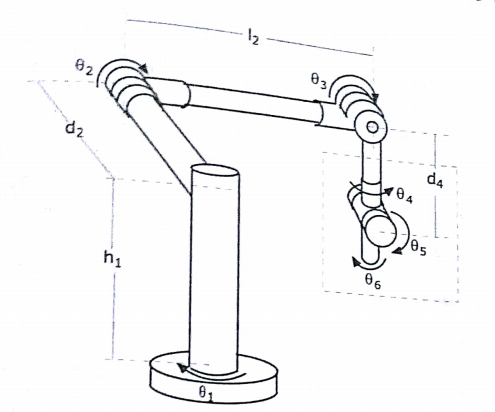
Denklem 4.4'ten faydalanarak uç işlevcisinin kartezyen uzayda konumunu belirleyen ilk üç eklem değişkeni θ1 , θ2 ve θ3'ü bulalım. 6T = 2T.3T.4T.5T.6T ............... (4.36) Dönel eklem değişkeni θ1, denklem 4.36'daki (2,4) karşılıklı matris elemanlarının eşitlenmesiyle bulunur. θ1 = NaN ............... (4.37) Dönel eklem değişkeni θ3 denklem 4.36'daki (1,4), (2,4) ve (3,4) karşılıklı matris elemanlarının eşitlenmesiyle ve karelerinin alt alta toplanmasıyla bulunur. θ3 = NaN Dönel eklem değişkeni θ2, denklem 4.36'daki (1,4) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ2 = NaN ± NaN Denklem 4.6'ten faydalanarak uç işlevcisinin kartezyen uzayda yönelimini belirleyen son üç eklem değişkeni θ4 , θ5 ve θ6'yı bulalım. 6T = 4T.5T.6T ............... (4,40)
Rxyz( λ , β ) =

θ5 = ±NaN Dönel eklem değişkeni θ4, denklem 4.40'daki (1,3) ve (3,3) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ4 = NaN Dönel eklem değişkeni θ6, denklem 4.40'daki (1,1) ve (2,2) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ6 = NaN Bu robotta 6 tane dönel eklem olmasına rağmen son üç eklem bir noktada kesiştiğinden çözüm kümesi sayısı 64 yerine 16'dir. Şekil 4.11'de verilen her çözüm kümesinde θ1'den başlayıp θ6'ya kadar takip edilebilecek her bir yol bir çözüm kümesini temsil etmektedir.

-θ1 = NaN           +θ1 = NaN -θ3 = NaN                 +θ3 = NaN -θ2-4 = NaN           +θ2-3 = NaN           +θ2-2 = NaN           +θ2-1 = NaN θ5-8 = NaN      θ5-7 = NaN       θ5-6 = NaN      θ5-5 = NaN      θ5-4 = NaN      θ5-3 = NaN      θ5-2 = NaN      θ5-1 = NaN
θ4-8 = NaN      θ4-7 = NaN      θ4-6 = NaN      θ4-5 = NaN      θ4-4 = NaN      θ4-3 = NaN      θ4-2 = NaN      θ4-1 = NaN θ4-16 = NaN     θ4-15 = NaN     θ4-14 = NaN     θ4-13 = NaN     θ4-12 = NaN     θ4-11 = NaN     θ4-10 = NaN     θ4-9 = NaN
θ6-8 = NaN      θ6-7 = NaN      θ6-6 = NaN      θ6-5 = NaN      θ6-4 = NaN      θ6-3 = NaN      θ6-2 = NaN      θ6-1 = NaN θ6-16 = NaN     θ6-15 = NaN     θ6-14 = NaN     θ6-13 = NaN     θ6-12 = NaN     θ6-11 = NaN     θ6-10 = NaN     θ6-9 = NaN