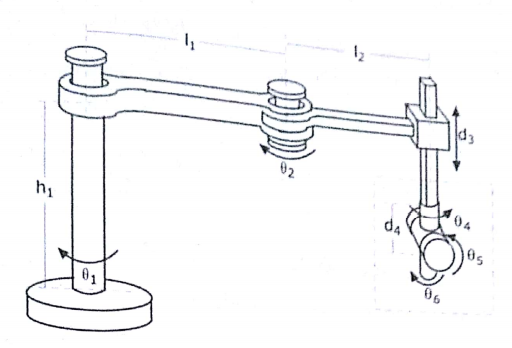
- Dönel eklem değişkeni θ1, denklem 4.44'deki (1,4) v2 (2,4) karşılıklı matris elemanlarının eşitlenmesiyle bulunur. θ1 = NaN° ............... (4.37) θ1 = NaN° ............... (4.37)
Görüldüğü gibi birinci eklem değişkeni için θ1 = NaN ve θ1 = NaN gibi iki farklı açı elde ettik. İkinci iklem değişkeni bulmak için birinci eklem değişkeninini θ1 = NaN alalım. - Dönel eklem değişkeni θ2'de denklem 4.44'deki (1,4) ve (2,4) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ2 = NaN° θ2 = NaN° Görüldüğü gibi birinci eklem değişkeni için θ2 = NaN° ve θ2 = NaN° gibi iki farklı açı elde ettik. İkinci iklem değişkeni bulmak için birinci eklem değişkeninini θ2 = NaN alalım. - Prizmatik eklem değişkeni d3 denklem 4,4'deki (3,4) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. d3 = h1 -Pz _ d4 . d3 = 0
Rxyz( λ , β ) =

Denklem 4.5'ten faydalanarak uç işlevcisinin kartezyen uzayda yönelimini belirleyen son üç eklem değişkeni θ4 , θ5 ve θ6'yı bulalım. 6T = 3T.4T.5T.6T ............... (4,40) - Dönel eklem değişkeni θ5, denklem 4.48'deki (3,3) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ5 = 180° θ5 = -180° Görüldüğü gibi birinci eklem değişkeni için θ5 = 180 ve θ5 = -180 gibi iki farklı açı elde ettik. İkinci iklem değişkeni bulmak için birinci eklem değişkeninini θ5 = 180 alalım. - Dönel eklem değişkeni θ4, denklem 4.48'deki (1,3) ve (2,3) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ4 = NaN° θ4 = NaN° Görüldüğü gibi birinci eklem değişkeni için θ4 = NaN ve θ4 = NaN gibi iki farklı açı elde ettik. İkinci iklem değişkeni bulmak için birinci eklem değişkeninini θ4 = NaN alalım. - Dönel eklem değişkeni θ6, denklem 4.48'deki (3,1) ve (3,3) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ6 = -180° θ6 = 0° Görüldüğü gibi birinci eklem değişkeni için θ6 = -180 ve θ6 = 0 gibi iki farklı açı elde ettik. İkinci iklem değişkeni bulmak için birinci eklem değişkeninini θ6 = -180 alalım.