Ex: 6
Şekilde eklem kaçılıklı bilekli altı serbestlik derecesine sahip bir robot veriliyor. Bu robotun ters kinematiğini çözüp çözüm kümelerini bulunuz.

Şekilde eklem kaçılıklı bilekli altı serbestlik derecesine sahip bir robot veriliyor. Bu robotun ters kinematiğini çözüp çözüm kümelerini bulunuz.
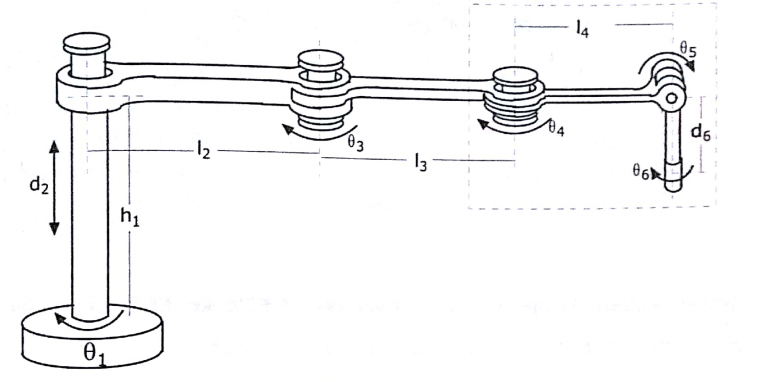
Denklem 4.9'dan faydalanarak iki, beş ve altıncı eklem değişkenlerini ( θ6 , θ5 ve d2 ) bulalım. 6T = 3T.4T.5T ............... (4,52) Rxyz( λ , β ) =
- Dönel eklem değişkeni θ6, denklem 4.52'deki (3.3) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. (3.3)............ Sθ6.r31 + Cθ6.r32 = 0 ise => θ6 = Atan2( -r32 , r31 ) veya θ6 = Atan2( r32 , -r31 ) ...................(4.53) θ6 = Atan2( -r32 , r31 ) için... => θ6 = -180° θ6 = Atan2( r32 , -r31 ) için... => θ6 = 0° - Dönel eklem değişkeni θ5, denklem 4.52'deki (3.2) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. (3.2)............ Cθ5 = -r33 θ5 = Atan2( ± 0 , 1 ) .............(4.54) + işareti için => θ5 = 180° - işareti için => θ5 = 180° Prizmatik eklem değişkeni d2, denklem 4.52'deki (3,4)karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. (3.4)............ -r33.d6 +Pz -d2 = 0 ise => d2 = Pz -r33.d6 => d2 = 0 Denklem 4.4'ten faydalanarak bir, üç ve dördüncü eklem değişkenlerini ( θ1 , θ3 ve θ4) - Dönel eklem değişkeni θ1, denklem 4.56'daki (1,4) ve (2,4) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ1 = Atan2(p,q) = 0 ± Atan2(sqrt(P^2+q^2-y^2),-y) = 0 .............(4.59) + işareti için => θ1 = 0° - işareti için => θ1 = 0° Denklem 4.57'den faydalanarak dördüncü eklem değişkeni θ4 aşağıdaki gibi bulunur. θ4 = Atan2( ± 1 , 0 ) .............(4.60) + işareti için => θ4 = 90° - işareti için => θ4 = -90° - Dönel eklem değişkeni θ3, denklem 4.52'deki (2,2) karşılıklı matris elemanlarının eşitlenmesiyle aşağıdaki gibi bulunur. θ3 = Atan2( Cos(T4).Sin(T5) , Sin(T4).Sin(T5) ) = 0±Atan2(sqrt( Sin^2(T5)- (-Sin(T1).r13 + Cos(T1).r23) ),(-Sin(T1).r13 + Cos(T1).r23)) = 0 + işareti için => θ3 = 0° - işareti için => θ3 = 180°